前段时间,碰到一个陆海项目,我们提供的成果都是CGCS2000坐标。施工单位要求提供当地控制点,用来放样。按道理来说,我们不需要提供,因为项目是CGCS2000坐标,施工方只需要拿千寻CORS进行放样即可。即使有当地控制点,我们一般也不用,因为海边的控制点沉降非常厉害,我们曾经吃过很大的亏。有个同事有几个当地的控制点,刚好也测了CGCS2000坐标,基于给甲方提供良好服务,我们也提供了。博主用高程异常看了一下这几个控制点,沉降不明显。
按照惯例,先说结论:
(1)三参数转换模型用于坐标转换时,当区域边长跨越小于 30' 时,X、Y、Z 方向的转换中误差均未超过 10 mm ;当区域边长跨越未超过 40' 时,其最大转换误差为 20 mm ;区域边长跨越达到 60' 时,其 Z 方向转换误差为 30 mm,超出了坐标转换的精度要求。布尔莎四参数、六参数模型的转换精度在全国区域范围内适用 ;布尔莎七参数模型适用于全球范围的坐标系统转换。
(2)三参数法不合适长条带测量或大面积(区域)的 RTK 测量,也不利于相邻测区的数据衔接,只适宜于小范围测区测量,其优点在于只需有 1 个点即可获得转换参数。三参数坐标转换模型,点位误差和高程误差与基准点的距离成正比,在 10 km 范围内,点位误差为 0.1m左右,高程误差小于 0.2m; 在距离 20 km 范围内,点位误差小于0.2m,高程误差小于0.5 m。
(3)七参数法在适用范围更加广泛,当外延区域较大时,其转换的平面精度仍然较高。但通过上述数据,本文建议可采取分区进行转换,以保证高程的转换精度。七参数法在参与计算的控制点选择上要特别注意所选点尽量避免在近似一条直线上,通过对本文实例的分析可得,无论是选择 3 个点或者多个点求解七参数,其转换结果基本相同。
三参数坐标转换模型转换精度的研究_符建波
由模拟计算结果及实例验证数据分析可得: 三参数坐标转换模型,点位误差和高程误差与基准点的距离成正比,在 10 km 范围内,点位误差为 0.1m左右,高程误差小于 0.2m; 在距离 20 km 范围内,点位误差小于0.2m,高程误差小于0.5 m。当然,该结论仅仅是针对某一地区的统计结果且只是进行了数据统计,没有进行严密的公式论证,对于其他地区的情况及论证工作,还有待进一步研究。
文中举了2个例子,实例1是平地,实例2是山区
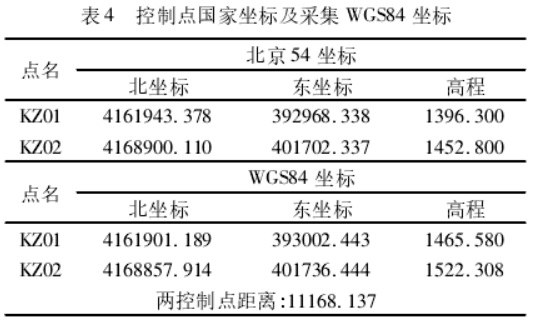
【实例1】某工区地形平坦,地形起伏在 50 m左右,高程异常变化较小,因此在小范围内三参数转换能获得较高的高程精度。
以控制点 KZ01 为基准点进行三参数计算。参数计算结果如下:
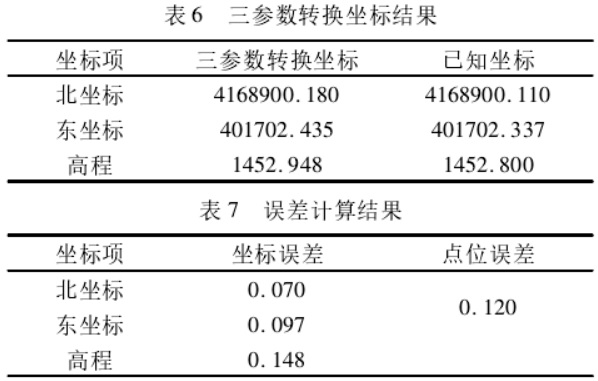
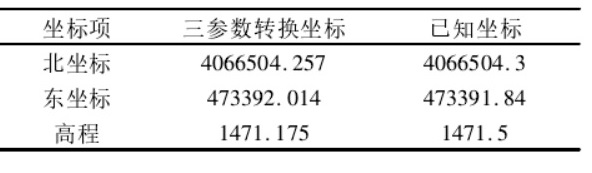
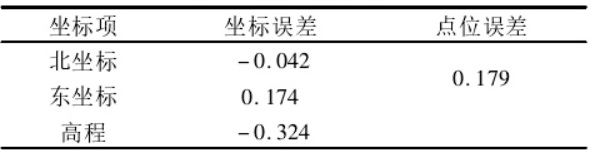
由三参数转换得到 KZ02 的国家坐标及误差如表 6 和表7所示。
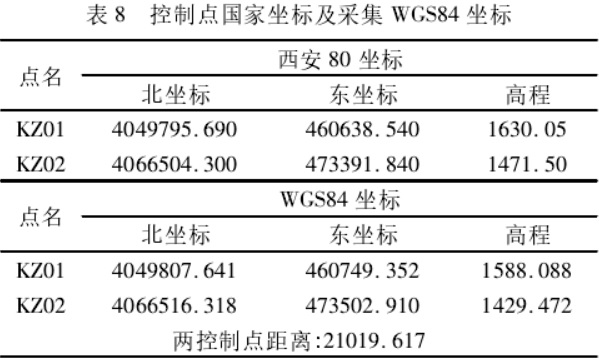
【实例2】某工区位于山区,高差在 200 m 左右,高程异常相对实例一所在工区较大。控制点国家坐标及采集WGS84 坐标见表 8。
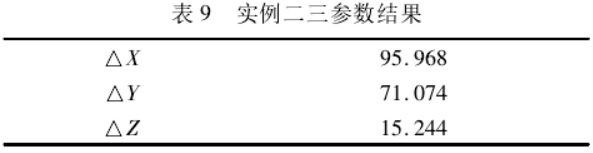
以控制点 KZ01 为基准点进行三参数计算。参数计算结果如下:
由三参数转换得到 KZ02 的国家坐标及误差见下表所示。
从上面控制点可以看出,三参数计算的源坐标是西安坐标(经度、纬度和水准高),目的坐标是WGS84坐标(经纬、纬度和椭球高)。
坐标系统转换模型的选择及精度分析_胡承舟
文中对三参数、七参数的计算和使用有大量实例。
本文采用某地的 D 级 GPS 控制网中一组数据(包含 18 个控制点),利用数据转换软件 pinnacle(注:Topcon GPS数据处理软件),分别进行三参数和七参数坐标转换,并将所得结果用 TGO 软件中的点校正功能验证,所得精度可精确到毫米级。所以本文所有数据均采用 pinnacle 的换算结果,分析三参数法和七参数法各自的适用范围和优点。由于工程中常用数据为高斯平面坐标和高程,所以本文也相应的对平面和高程进行三维转换分析,以求达到最实用的效果(该区采用 1954 年北京坐标系,1985 国家高程基准)。
三参数法转换结果及精度分析
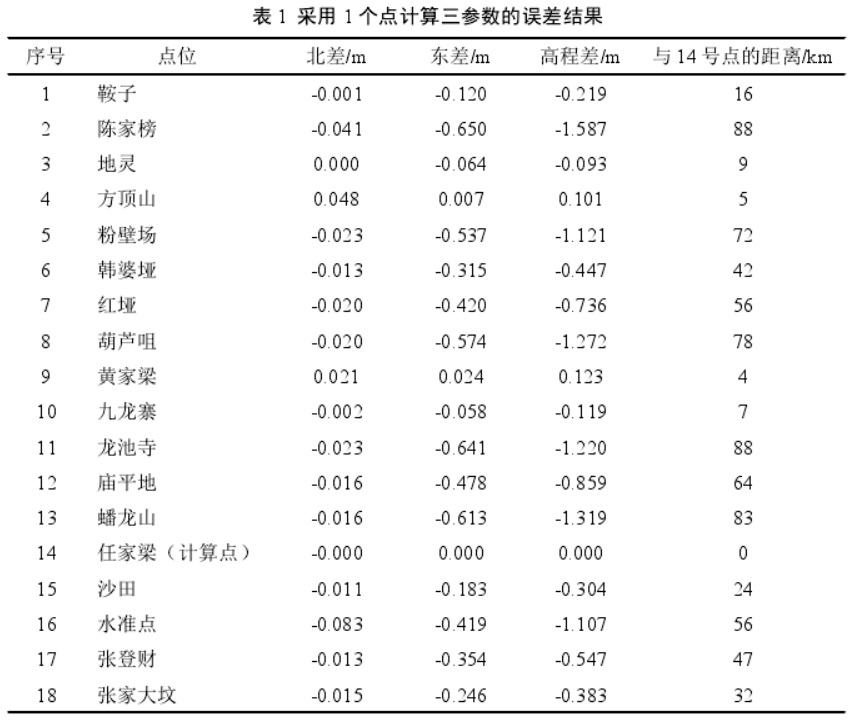
当采用 1 个点计算得到的三参数对 D 级网中其他控制点进行坐标转换,并与已知坐标对比,位于 14 号点的 10km 范围内的 3、4、9、10 号点,平面差值<10cm,高程差值<20cm。而在 10km 外(除 3、4、9、10 号点外的其他点),随着距离越远,差值越大,平面和高程差值均在 20cm以上,已经不符合 1:2000 图根控制测图要求。
七参数法转换结果及精度分析
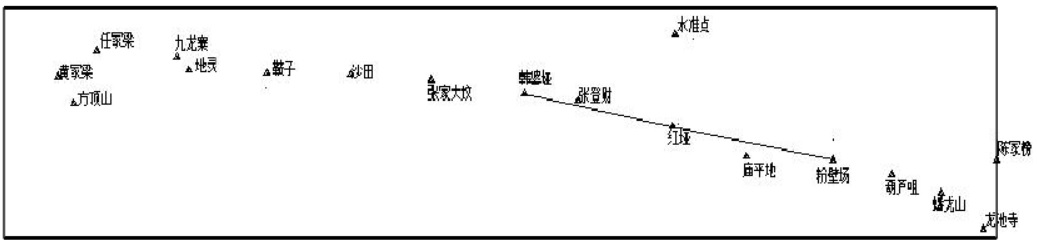
选点方式一:选取近似在同一直线上 3 个点计算七参数,所选 3 个点位如图 1 所示。
选取如图 1 所示,近似在同一直线上 3 个点(粉壁场、韩婆垭、红垭)计算得到的七参数如下:
三个平移参数:DX = -153.858556 m DY = -1506.49838 m DZ = 1907.924541 m
三个旋转参数:RX = 75.65793197 " RY = 12.23938172 " RZ = 14.52389411 "
尺度比因子:7.367085236 ppm
采用近似在一条直线上的 3 个点计算得到转换参数中,平移量和旋转角度较大。从表 2 中可以看出,用该参数转换其他控制点坐标时,与已知坐标差值较大,尤其是高程差值远大于平面,所得结果不符合规范要求。因此在求解七参数时,应尽量避免选取近乎在同一直线上的点位。
选点方式二:选取构成三角形的 3 个点计算七参数,其所选取的点位大致如图 2 所示:
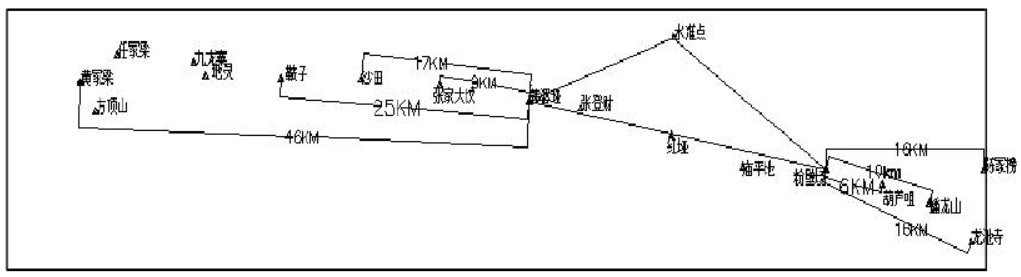
选取如图 2 所示构成三角形的 3 个点(粉壁场、韩婆垭、水准点)计算得到的七参数如下:
三个平移参数:DX = -124.7563197 m DY = -362.9833077 m DZ = 141.3846751 m
三个旋转参数:RX = 9.491499487 " RY = -0.8340208849 " RZ = 4.975141594 "
尺度比因子:7.476187361 ppm
根据表3 中的数据分析可知,其转换结果无论是平面还是高程精度均明显优于 “选点方式一”的转换结果。所有平面转换结果与已知坐标差值均<5cm,即使距离所选计算点 46km 处的控制点(黄家梁),差值仍在 5cm 之内。在这三点构成的三角形包含范围内及其外延 5km 以内,其高程转换精度仍可达<5cm,如庙平地(1km),葫芦咀(6km);对于包含范围的外延 10km 以内,高程转换精度<20cm,可达到 1:2000图根控制测量要求。
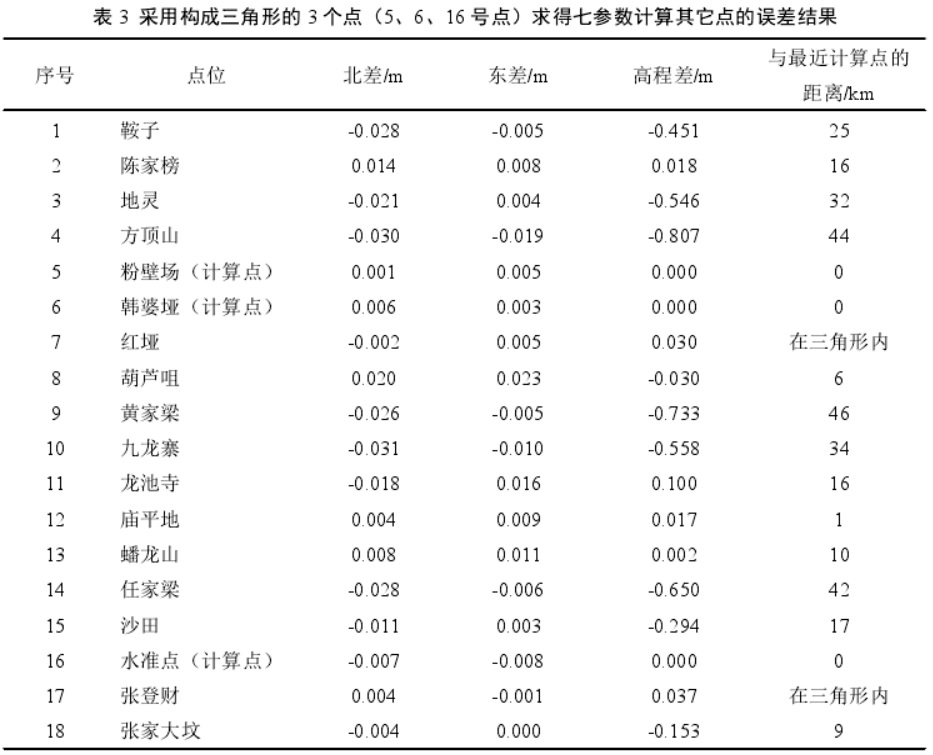
选点方式三:选取构成多边形的 5 个点计算七参数,其所选取的 5 个点位如图3 所示:
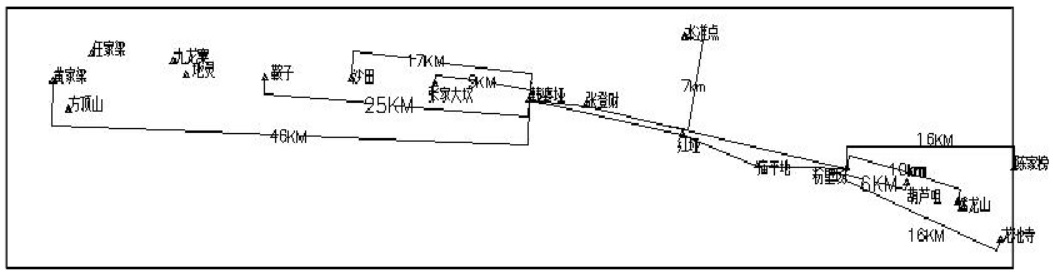
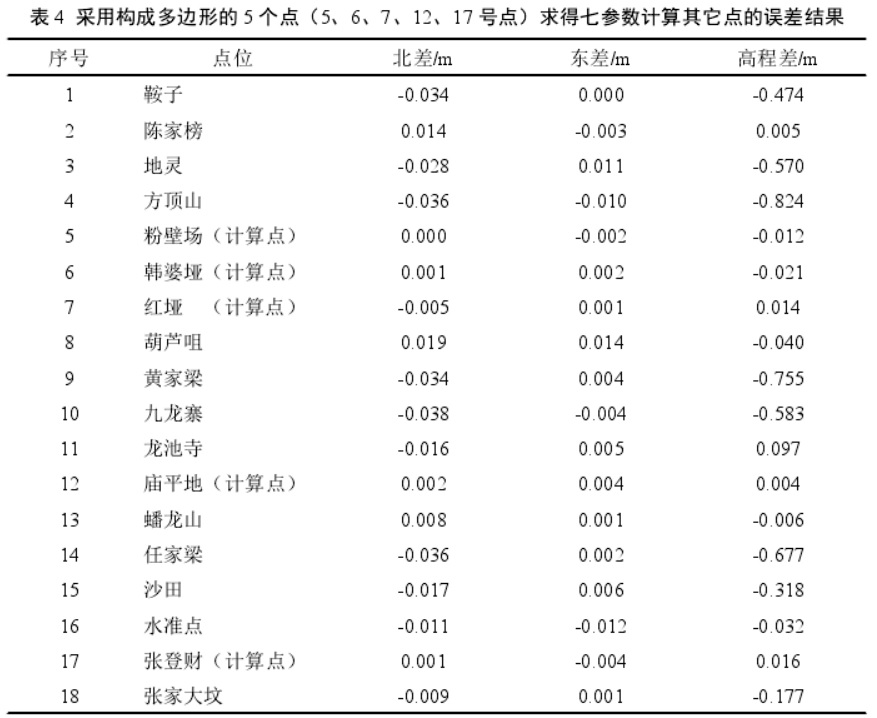
根据如图 3 所示选取的 5 个点(粉壁场、韩婆垭、红垭、庙平地、张登财)计算七参数如下:
三个平移参数:DX = -126.7350349 m DY = -355.6334487 m DZ = 131.7399662 m
三个旋转参数:RX = 9.115546039 " RY = -0.9548473604 " RZ = 4.962235383 "
尺度比因子:7.250265579 ppm
通过七参数转换实例可以得出如下共同点:与三参数法相比,七参数法的适用范围更大。选点方式二、三两种求解七参数法得到平面精度基本一致,距离所选计算点 46km 处点位的平面精度仍优于 5cm;从高程精度方面分析,距离所选计算点 10km 外的多数点高程误差可达到 20cm 以上,达不到 1:2000 图根控制要求,如 1 号点鞍子(25km )高程差值为 0.474m。为了实际应用方便,本文建议尽量选取涵盖测区的点位求解七参数,这样对整个测区数据的衔接和统一比较方便。
结论及建议
1、三参数法不合适长条带测量或大面积(区域)的 RTK 测量,也不利于相邻测区的数据衔接,只适宜于小范围测区测量,其优点在于只需有 1 个点即可获得转换参数。
2、七参数法在适用范围更加广泛,当外延区域较大时,其转换的平面精度仍然较高。但通过上述数据,本文建议可采取分区进行转换,以保证高程的转换精度。
3、七参数法在参与计算的控制点选择上要特别注意所选点尽量避免在近似一条直线上,通过对本文实例的分析可得,无论是选择 3 个点或者多个点求解七参数,其转换结果基本相同。
4、为方便 RTK 作业设站和进行测量,在转换参数控制点选择上,所选的控制点尽量合理均匀,覆盖面要大,同时选取的计算点要便于架设 RTK 作业的基站,在求解转换参数后,务必加强检核。
5、在实际作业中,可通过对转换结果数据分析,对于超出该区七参数作业范围时,务必进行控制网的补测,并重新求解七参数,以便保证测量精度。
三参数与四参数转换模型适用性研究_倪飞
通过精度转换算例验证了不同参数转换模型的精度情况。三参数转换模型用于坐标转换时,当区域边长跨越小于 30' 时,X、Y、Z 方向的转换中误差均未超过 10 mm ;当区域边长跨越未超过 40' 时,其最大转换误差为 20 mm ;区域边长跨越达到 60' 时,其 Z 方向转换误差为 30 mm,超出了坐标转换的精度要求。布尔莎四参数、六参数模型的转换精度在全国区域范围内适用 ;布尔莎七参数模型适用于全球范围的坐标系统转换。在实际的工程应用中,应针对转换区域情况选择适当的转换模型。
布尔沙七参数转换公式
七参数转换:三个平移参数、三个旋转参数和缩放参数
三参数转换:只考虑三个平移参数
四参数转换:不考虑三个旋转参数
以上X、Y、Z都是空间直角坐标,是根据大地坐标(经度、纬度和大地高)计算出来的,公式如下:
式中,N 为椭球卯酉圈曲率半径; a 为椭球长半径; e为椭球的第一偏心率
关于布尔沙公式计算的源坐标和目的坐标
使用布尔沙公式计算三参数或者七参数的应用场景,主要发生在当地项目是北京54坐标或者西安80坐标的情况。转换公式如下:
从上面的公式可以看出,空间直角坐标是由大地坐标计算出来的。而在实际的生产过程中,我们拿到的地方控制点,无论是北京54还是西安80,多半是高斯投影后的平面坐标和1985国家高程。先通过高斯投影反算将平面坐标转成大地坐标,然后将1985高程当做大地高进行计算。目的坐标现在都是CGCS2000,通过千寻CORS测出来的,得到大地坐标和大地高。得到了控制点的源坐标和目的坐标,就可以通过布尔沙公式计算转换三参数和七参数。

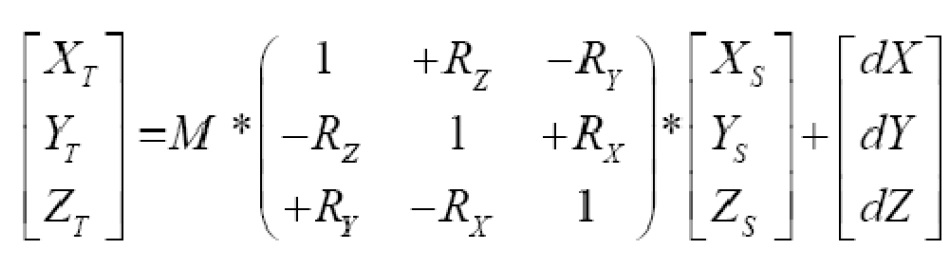
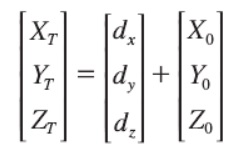
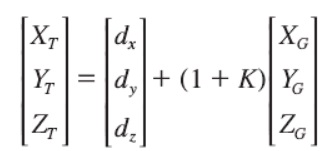
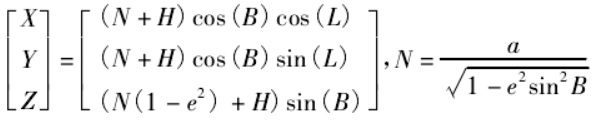
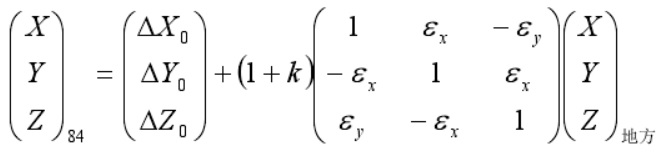

首先我认识到布尔莎七参数的作用对象是不同地心空间直角坐标系的坐标,即基于某个椭球的球心为原点,指向北极为 Z 轴,指向本初子午线+赤道交点为 X 轴。
我参考了一些博客的测试数据,基于 python3 的 pyproj、numpy、scipy 库,对输入的控制点对直角坐标数组进行了最小二乘解算超定方程组,基本能达到参考博客的结果(误差较小,可以认为是编程语言、数学库和浮点数的偏差,均可接受)。
但是,这个程序对输入数据是大地坐标(经纬高,epsg4326),目标坐标系是 gk 投影坐标(北京 54 或西安 80,3 度分度带)的情况时,却不能达到千寻手簿或笑脸软件(COORD GM)的结果,偏差很大。
哪怕反过来算也达不到手簿或笑脸软件的值,手簿和笑脸软件的结果是基本一致的,所以我想请教一下思路是否有问题。
我的计算思路是,把源坐标点和目标坐标点都通过 pyproj 重投影到对应椭球的地心世界坐标,然后调用最小二乘函数进行解算七参数。
感谢!