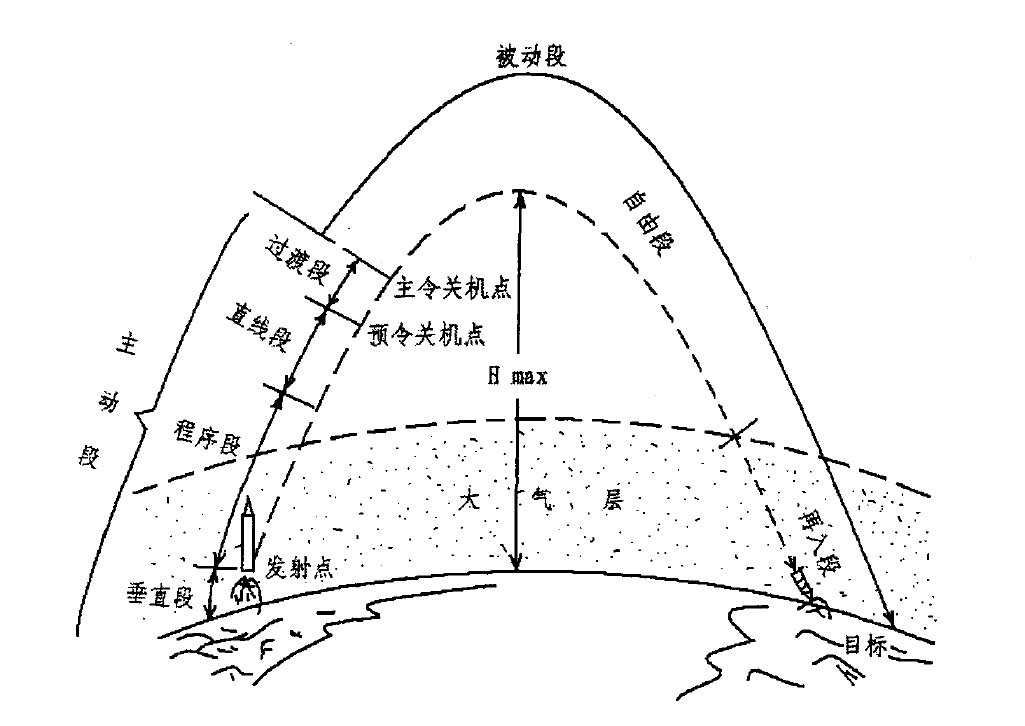
根据远程飞行器在飞行中的受力情况,一般将飞行轨迹划分为主动段和被动段,前者是指从发射平台起飞到发动机主令关机点的一段飞行轨迹,后者是指从发动机主令关机点到飞行器着陆的一段飞行轨迹(又分为自由段和再入段)。在飞行轨迹的主动段,飞行器除了受到发动机推力和控制系统的调控作用外,还会受到空气动力、地球引力和由地球自转引起的惯性力的影响。而在被动段,飞行器则完全依靠在主动段终点获得的动能飞行,不再受发动机推力和控制系统的调控作用。
因此,飞行器落点的精确度主要取决于控制系统在主动段终点获得的飞行器运动参数的可靠性。但确定运动参数的准确性又完全取决于飞行器在飞行过程中的受力分析、建模和计算。随着飞行器制造工艺和控制技术的不断突破和完善,地球重力扰动场(在地球外部空间的任意点,实际引力加速度不同于正常引力加速度,因而实际重力也不同于正常重力,称实际引力场与正常引力场的差为地球扰动引力场,实际引力加速度与正常引力加速度之差为扰动引力加速度,简称扰动引力。)计算误差已经成为限制飞行器落点精度进一步提高的主要因素。
导弹在发射阵地上空近地低速飞行时,对地球重力场的高频信息非常敏感,由重力场引起的加速度误差会很快积累成速度误差,成为导弹脱靶因素;当导弹进入高空高速飞行阶段,制导系统对高频重力场信息的敏感性逐渐减小,而与地球重力场的中、长波信息的相关性逐渐增大。因此,要想有效控制导弹的落点偏差,必须首先解决地球外部空间特别是近地空间扰动引力场的精密计算问题。
地球重力场对飞行器落点精度的影响主要体现在两个方面:
①飞行器的初始定位(也称为初始化阶段);
②飞行器的飞行控制。
飞行器发射前必须对载体和控制系统传感器进行精确的垂直定位和定向,以建立制导坐标系。由于飞行器在发射台竖直及惯性系统标定过程中都是以发射点的铅垂线为基准的,而飞行轨迹计算则是以发射点椭球法线为基准的发射坐标系作为参照系。因此,如果不对两者之间的差异(即垂线偏差)进行修正,必然会引起飞行器落点的偏差。理论分析和实际计算都表明,垂线偏差对飞行器落点的影响不仅与其量值大小有关,而且随发射点位置、射程和航向角的改变而变化。
对于1万km左右射程的飞行器,1"垂线偏差的影响量一般不超过 50m。在飞行器的初始化阶段,除了载体的姿态影响因素外,发射点位置误差特别是高程分量误差对飞行器落点的影响也不容忽视。高程分量误差主要体现为高程异常计算误差其影响大小既与飞行器的射程有关,又与飞行器的飞行轨道特性有关。根据理论分析估计,1m高程异常误差对飞行器落点的影响一般不超过15m。
在空中飞行阶段,飞行器始终受到地球重力异常场的作用,当计算飞行轨道使用的引力场模型存在误差时,也必然会引起飞行器落点产生一定的偏差,其影响量主要取决于飞行器射程大小和扰动引力场沿飞行轨迹的变化激烈程度。
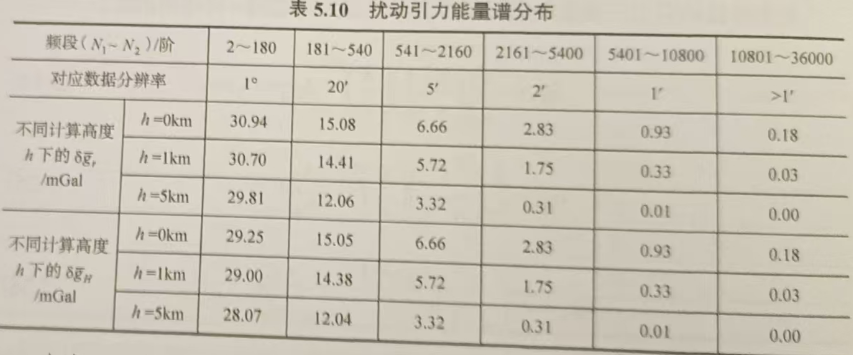
由上表可知,如果忽略几十毫伽最值的扰动引力的影响,那么可能给远程飞行器带来千米级的射程偏差。扰动引力场除了影响飞行器的主动段飞行外,对被动段飞行也会产生不可忽略的影响,但由于被动段飞行轨迹离地面较高,通常在200km以上,与主动段相比,一方面扰动引力场对被动段飞行的作用相对会减小,另一方面高空扰动引力的计算误差也相对容易控制。因此,在实际应用中,一般都以主动段扰动引力的计算精度要求作为地面或海面重力测量技术设计的基本依据。
根据当前及今后一个时期飞行器技术的发展水平和实际应用需求,可将扰动引力场单一要素对1万km 以上射程的飞行器落点偏差影响量限定为100m。由上表的计算结果可以看出,如果以100m为限差量,那么扰动引力计算精度的要求应设定为:优于4mGal。
下图是扰动引力能量谱分布,扰动引力精度如要满足4mGal的要求,则重力的分辨率最好到2'。
但由于在靠近发射点的低空段求得高精度的扰动引力参数要比高空段困难得多,在重力场变化激烈的区域要比变化相对平缓的区域困难得多。因此,对于扰动引力的计算精度要求,在不同区域、不同高度应有所区别,“优于 4mGal”可理解为一种平均精度要求。又由前面的论述可知,1m高程异常误差对飞行器落点的影响一般不超过15m,1"垂线偏差的影响量一般不超过50m。
显然,在当前的技术条件下,高程异常的计算精度完全能够满足飞行器落点偏差100m的限差要求。而对于垂线偏差参量,根据重力场参数之间的泛函关系,2"垂线偏差的误差量相当于扰动引力水平分量10mGal 的偏差,这个量值已经远远超过前面的扰动引力4mGal的精度要求。由此得知,只要确保扰动引力的计算精度满足“优于4mGal”的要求,那么2"垂线偏差的计算精度要求也自然能够得到保障。
根据大地水准面与垂线偏差的关系,设计合理的计算方案,给出利用大地水准面模型计算垂线偏差的简化公式,并通过模拟计算探讨大地水准面相对精度、取点间距和已知点选取及个数对计算结果的影响。利用GEOID12B模型分别计算GSVS2011、GSVS2014项目中各测站点和美国西部区域(40°~45°N,100°~105°W,分辨率为1')的垂线偏差,并与GSVS项目垂线偏差实测值和DEFLEC12B模型值进行比较。结果表明,垂线偏差南北分量和东西分量的计算精度均优于±0.5″,说明利用相对精度为cm甚至亚cm级的大地水准面模型可获取较高精度的垂线偏差。
要想确保地球重力场单一扰动要素对空间飞行器落点的影响不超过 100m的限差,扰动引力三分量的计算精度必须优于4mGal,由此求地球表面重力异常观测量的数据分辨率应不低于2'x2',网格平均重力异常精度应优于 5mGal。这样的要求对地面测点和海面测线布设又提出了什么样的量化约束指标,是本专题研究接下来需要研究解决的核心问题。
网格数据精度既与重力异常的观测精度有关,又与计算网格内布设测点的数量和均匀度有关,前者主要取决于测量传感器的技术性能和作业模式,后者主涉及作业效益和工作难度,取决于测量区域重力场的变化复杂程度。人们习惯上将后者称为网格数据的代表误差。在陆地区域由于重力观测误差远小于网格平均值的代表误差,所以在讨论网格数据精度时般忽略前者的影响。但在海洋区域,受测量动态效应的影响,重力观测误差明显增大,通常可达1~2mGal,因此在讨论海洋重力网格数据精度时,必须同时顾及观测误差和代表误差的影响。
为了保证海洋 2'x2'网格平均重力异常精度优于5mGal,比较稳妥的重力测线布设方案应当是:在1类和2类海区,在2'x2网格中央布设1条测线;在3类和4类海区,在2'x2'网格内均匀布设2条测线。《海洋重力测量规范》(GJB 890A一2008)规定的重力测线布设密度指标为:飞行器发射首区测线间隔1',常规测量测线间隔2'。由此可见,在某种意义上,本专题研究给出的布设方案与《海洋重力测量规范》(GJB890A-2008)的规定是相吻合的,前面的分析论证也从另一个侧面证明现行作业规范规定的测线布设密度指标是合理可行的。
小结
(1)地球重力扰动对远程飞行器的飞行轨迹具有不可忽略的影响,几十毫伽量值的扰动引力可给远程飞行器带来千米级的落点偏差;如果以100m作为飞行器落点偏差的限差量,那么扰动引力计算精度的限定指标应优于4mGal。
(2)要想使扰动引力的计算精度达到4mGal限定指标,地面重力异常的观测分辨率至少应当精细到 2'x2',相应网格平均重力异常的测量精度应优于5mGal。
(3)要想使2'x2'网格平均重力异常的计算精度达到5mGal限定指标,在地形变化比较平坦的1类(平原和丘陵)和2类海区(小山和中山区),应在2'x2'网格内至少布设1条海洋重力测线;在地形变化比较激烈的3类(大山区)和4类海区(特大山区)),应在2'x2'网格内至少布设2条海洋重力测线。
参考文献:
1、扰动引力的快速计算及其对落点偏差的影响_王昱2002
2、自由段重力异常对弹道精度的影响_段晓君2002
3、重力场对弹道导弹自由段落点影响的仿真分析_冯伟2009
4、扰动引力对弹道导弹落点影响分析_李晓燕2008
5、弹道导弹落点精度影响因子分析_施岩龙2016
6、重力场对飞行器制导的影响及海洋重力测线布设_黄谟涛2016
7、利用大地水准面模型计算垂线偏差的方法及精度分析_李伟超2019



发表评论: