大地水准面是代表地球形状的一个封闭重力等位面,理论上定义为与全球无潮平均海平面密合的重力等位面,并用这个等位面相对于一个选定的参考椭球(一般选用平均地球椭球)的大地高描述它的起伏,形成一种实用化的网格数值模型或以位系数表达的解析函数模型。
可采用两种方法对大地水准面进行定位和精化:一种是直接测量法;另一种是间接计算法。
直接测量法是指根据确定的几何关系直接测定某点大地水准面相对参考椭球面的高程或两点之间的大地水准面高差,采用天文水准、天文重力水准或 GNSS水准确定大地水准面的方法均属于直接测量法;
间接计算法是指以一种或多种重力数据源为边值条件,建立关于重力扰动位的大地测量边值问题,通过求解边值问题确定扰动位函数,再由Bruns 公式换算为大地水准面高。为了区别起见,通常把由重力观测数据间接计算得到的大地水准面称为重力大地水准面,由此方法获得的大地水准面高一般都是相对于全球地心坐标系中的平均地球椭球面,故也称其为绝对大地水准面。
针对大地测量边值问题(比如说已知地球表面的重力观测值(即边值条件),求地球表面和外部空间的重力调和函数)的求解理论和方法研究,国际上经历了跨越100多年的三个主要发展阶段,分别聚焦不同的边界面,先后诞生了3种著名的大地测量边值理论,即 Stokes边值理论、Molodensky 边值理论和 Bjerhammar 边值理论,3种理论分别给出了3种相对应的边值问题解式,依次为Stokes积分、Molodensky 级数解和 Bjerhammar广义Stokes积分。它们都属于解析法。
为保证扰动位在大地水准闻外满足调和性假设,Stokes边值理论要求大地水准面外部无地形质量,因此必把其外部的地形质量移去。因无论用何种方式移去地形质量都将使大地水准面发生变化,产生间接影响,故由Stokes积分计算得到的大地水准面是调整后的大地水准面。从理论上讲,只要地形重力归算及其间接影响考虑周密,各类不同的地形质量调整方案都能给出比较一致的Stokes积分解。目前,在实践中应用比较广泛的地形质量调整方案是Helmert第二类凝集法,其相对应的边值问题解称为Stokes-Helmert方法。考类到移去地形质量都需要已知地形质量的密度分布,地形质量密度假设偏差带来的不确定定性自然就成为Stokes 边值理论的主要缺陷。
Molodensky边值理论不需要整地形质量,因此 Molodensky级数解在理论上是严密的,但由于高阶项计算程的复杂性和不稳定性,实践中一般只考虑到级数的一阶项,至多考虑到级数的二阶项。
Bjerhammar 边值理论也不存在地形质量调整问题,不需要进行地效应改正和补偿处理。实际上,Bjerhammar 边值理论可以看作一类广义的等场源方法,此类方法不需要调整地形质量,但在地 面观测与等效场源之间的转换过程中已经巧妙地顾及了地形效应的影响,因此具有理论上的严密性。
1、基于 Stokes 边值理论的计算模型及数值检验
以我国陆地一个4°✖4°区块(32.5°N~36.5°N,102.5°E~106.5°E)为试验区,选用EGM2008位模型模拟产生大地水准面上的2'×2'网格重力异常及大地水准面高度的真值。该区块属于地形变化幅度相对较大的中等山区,试验效果具有一定的代表性。选用EGM2008位模型的前360阶作为参考场模型,计算网格重力异常和地水准面高度。
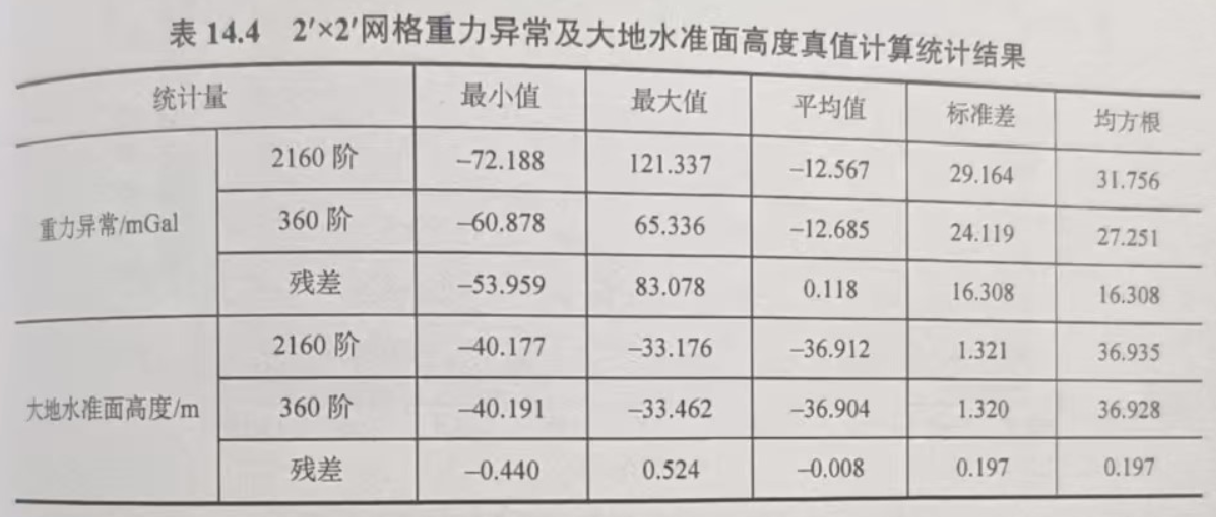
2'×2'网格重力异常及大地水准面高度真值计算统计结果如下。
下图是2160阶EGM2008位模型重力异常分布图。
在不考虑数据归算和观测误差影响条件下,要想将数据截断误差对大地水准面计算结果的影响控制在1cm以内,必须采用精细到 1'x1'分辨率的基础网格数据,同时还要将数据观测误差控制在 5mGa以内。
2、基于 Molodensky 边值理论的计算模型及数值检验
在使用Stokes边值理论之前,必须将这些观测值归算到海平面(即大地水准面)上。这就意味着,要知道大地水准面以外的物质密度,而精密观测这种密度分布是极其困难的,只能近似地采用已知的地形平均密度。此外,即使确定了物质密度的分布情况,由于重力归算使地形质量迁移,也会使所确定的大地水准面产生变形,即产生间接影响。
为了弥补 Stokes 边值理论的缺陷,Molodensky于1945 年提出了一种全新的研究地球形状及其外部重力场的理论和方法,其目标是采用地球表面上的重力观测数据直接确定地球自然表面形状。
Molodensky 问题可具体表述为:已知地球自然表面上所有点的重力位和重力向量,要求确定地球自然表面及其外部重力位。Molodensky问题的主要着眼点是要避开传统Stokes边值理论需要地壳密度假设的缺陷,建立新的更加严密的地球形状和外部重力场理论。Molodensky 问题及其解算方法一直是现代物理大地测量学研究的前沿领域,在理论大地测量学研究中起根本性的作用。
以我国陆地一个4°✖4°区块(32.5°N~36.5°N,102.5°E~106.5°E)为试验区,选用EGM2008位模型模拟产生大地水准面上的2'×2'网格重力异常及大地水准面高度的真值。地形高度数据采用两组数据源:一组由2160阶的球谐函数展开式 DTM2006 计算得到;另一组则依据重力异常与地形高度呈线性关系假设,由2160阶EGM2008位型计算得到的2'x2网格重力异常 Δg 反解得到。选用EGM2008位模型的前360阶作为参考场模型,计算网格重力异常、高程异常。
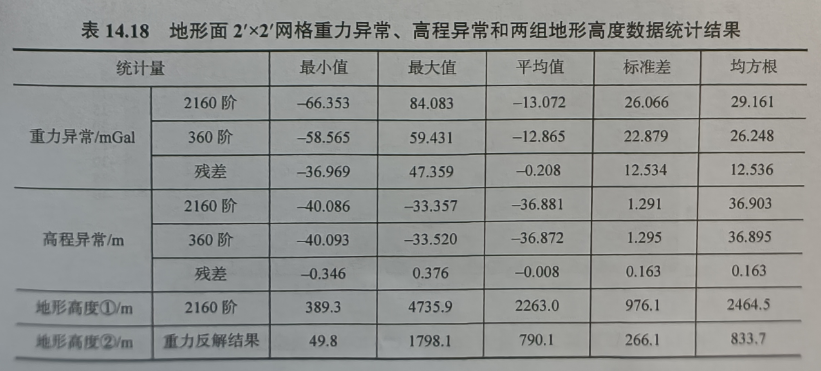
2'×2'网格重力异常、高度异常和两组地形高度数据统计结果如下。
3、基于 Bjerhammar 边值理论的计算模型及数值检验
针对 Srokes 边值理论存在的缺陷,Bjerhammar(1964)提出了一种以某虚拟球面为边界面,将大地测量边值问题转换为该球面外部边值问题的理论,又称为 Bjerhammar边值理论。分布在地球表面的一组重力异常观测值,可对应于地球内部无穷多个不同的虚拟重力异常场源,人们可通过不同的数学形式构造不同类型的等效场源,使其产生等效的位函数能够一致逼近地球外部真实的位函数。
Bjerhammar边值理论的解算思路是:以分布在地球表面上的一组离散重力异常为已知条件、将其向下调和延拓到一个完全处于地球内部的 Bjerhammar球面,在该球面上构造一个虚拟的重力异常场,并强制该虚拟场在地球表面及其外部空间产生的位与由已知的地球表面重力异常场产生的真实位一致,从而将地球表面边值问题等价地转换为一个简单的虚拟球面边值问题。Bjerhammar边值理论最终以最简单的 Stokes 积分公式给出问题的解,同时以一种隐含的方式顾及了地形效应的影响,这正是该理论的巧妙之处。
以我国陆地一个4°✖4°区块(32.5°N~36.5°N,102.5°E~106.5°E)为试验区,选用EGM2008位模型模拟产生大地水准面上的2'×2'网格重力异常及大地水准面高度的真值。地形高度数据由2160阶的球谐函数展开式 DTM2006 计算得到。选用EGM2008位模型的前360阶作为参考场模型,计算网格重力异常、高程异常。
2'×2'网格重力异常、高度异常和地形高度真值数据统计结果如下。




发表评论: