1、自由移站法的核心是大旋转角坐标转换的平差算法
2、大旋转角坐标转换方法有三种:七参数法,罗德里格矩阵,简便算法
3、七参数法是一种 局部最优算法,它的好坏取决于初始值
4、罗德里格矩阵摆脱了七参数法的三角函数,在初始值相同的情况下,精度比七参数法略差
5、简便算法其实是13参数法,七参数法的一个变种,参考了罗德里格的思想,易于编程
潘国荣等《工业测量三维基准转换参数的全局最优算法》2014年
摘 要:从全局最优的角度分析了工业测量空间三维基准转换时经常出现解不稳定现象的原因,利用最优初值和局部最优算法,可以获得唯一确定的全局最优解。结合实际工业测量应用中的公共点移站测量,用此方法可以获得更加稳定的转换参数,对于其他低信噪比平差问题出现解不稳定的现象提供了解决方法。
三维基准转换是测量领域中常见的一种数据处理方法,应用较为广泛。在大地测量中,旋转角为小角,常用布尔莎模型[1];而在工程及工业测量中,旋转角不一定是小角度,常采用 7 参数或 13参数模型[2]。在实际应用中,无论采用哪种模型,都会碰到解不稳定的情况,多数学者都是从病态的角度进行分析,提出了岭估计[3]方法、正则化[4]算法等,实际结果是用增加估值的有偏性来换取估值的稳定性。文献[5]通过引入正则化方法解决在布尔莎模型下的病态问题;文献[4]和文 献[6]分别从扰动性和参数相关性详细分析了病态问题的原因。总体来说,所谓参数解不稳定可理解为如果观测值有微小的变动,将会引起对未知参数求解的极大变化。在工业测量等小范围测区内,采集数据的信噪比普遍比较小,因此这种现象尤为突出。经研究认为,所谓求解出的参数会出现波动的结果,其实是在高斯最小二乘目标函数∑VTPV=min的情况下求解出的不同迭代初值附近的局部最优解,若采用求解全局最优解的处理方法则最终会得到稳定的全局最优解。
目前普遍流行的避免局部最优解的处理方法主要分两大类,一类是随机性算法,包括 GA(遗传算法)[7]和SA(模拟退火算法)[8]等;另一类则是确定性 算 法,主 要 有 区 间 方 法[9]和 填 充 函 数法[10]等。第一类随机性算法实际上只是一种改
进的局部算法,并不能保证所求的局部最优解就是全局最优解,而真正意义的全局最优解一定是唯一确定的[11-12]。但是已有的确定性全局最优算法普遍较麻烦,根据模型的不同列立的方式也会不同,而且运算量通常比较大。
本文利用全局最优初值结合成熟的局部最优算法,达到全局最优解算的目的,避免了直接利用复杂的全局最优算法,并以实例说明了此算法的方便性和可靠性,对于其他平差模型中出现解不稳定的情况提供了解决思路
4 结 语
本文从全局最优解的角度讨论分析了工业测量三维基准转换出现解不稳定情况的原因,将平移参数和尺度参数、角度参数分离,因而单独求解角度参数最优解近似值的数学模型简易许多,剔除了平移参数对解算角度参数的影响,求得的角度参 数 解 更 稳 定,得 到 并 验 证 了 在 一 个 整 区 间[-π,π]内,三个角度参数在解算坐标转换 7 参数中会有两个等价的全局最优解的结论,而如果不界定角度参数的范围,则有无穷多个等价解。
由于角度参数范围有界,本文采取枚举的方法获取其初值,属于一种确定性的全局最优解方法,也可以采取其他稳健的全局最优算法同时整体求解7个转换参数,替换本文分开求解的方法。在其他低信噪比的平差问题中出现解不稳定的现象时,可借鉴本文的方法。
潘国荣等《船舶测量自由移站法及多站转换参数的整体平差》2013年
摘 要:运用自由移站测量方法,将所有转换参数进行整体平差。对转换参数进行了精度分析,将整体平差前后的所有转换参数的精度进行了对比分析。实例计算和理论分析表明,此方法可提高各站间转换参数的精度,减少因为移站而造成的繁琐工作量。经过整体平差后,平移参数的精度为毫米级,旋转参数的精度为1″,满足船舶制造过程中的精度要求。
船舶建造的精度控制,就是以船体建造精度为基本准则,通过科学的管理方法和先进的工艺术手段,对船体建造进行全过程的尺寸精度分析与控制,以最大限度减少现场修正工作量,提高工作效率,降低制造成本,保证产品质量。根据船舶制造的特点和生产流程,通常将精度控制分为5个阶段,即放样阶段、加工阶段、部装阶段、分段装配阶段和船体搭载阶段,每个阶段的控制内容各有不同,要求也不一样。目前,国外先进国家在船舶制造过程中,已经基本达到内部构件无余量下料,全船分段无余量上船台合拢,而我国大多数船厂测量手段相对落后,应用软件开发能力与国外有相当大的差距,因而难以准确控制船舶制造过程中构件及船体的几何精度。近年来,我国在这方面投入较多的人力、物力进行研究,不断改进数据采集方法,提升数据处理能力。
目前,许多学者研究两个坐标系之间的转换关系,如文献[1]提出使用13参数方法计算大旋转角的三维坐标系转换参数;文献[2]提出使用罗德里格矩阵计算三维坐标系转换参数;文献[3]提出使用七参数坐标系转换模型计算盾构姿态的方法等。同时,也有学者对两个坐标系之间转换参数的精度和相关性进行了研究[4-6]。但是,这些工作都局限于两个坐标系之间转换参数的求取和精度分析。本文结合上述方法,研究了多个坐标系之间转换参数的求取及精度,结合船舶测量的特点,提出了自由移站方法和多站转换参数的整体平差方法。船舶测量中,采用自由移站方法进行数据采集,并通过数据的整体平差提高数据的精度。该方法的优势在于测站可以选择在任何合适的位置,不需要对中,对于分段体中无法观测到的点,可以选择任意合适的位置进行移站,通过移站前后所测公共点确定其测站坐标系,就可以把船舶分段体的特征位置在同一个坐标系里测定出来。
2 数据处理模型推导
2.1 附有约束条件的7参数模型
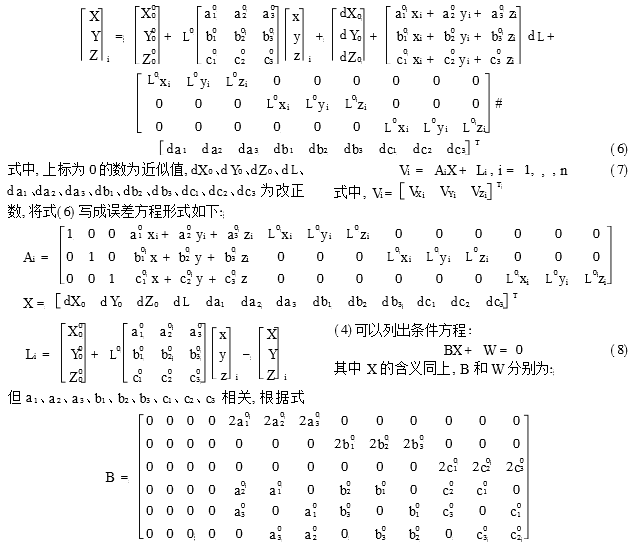
2.2 平差模型线性化
由于对式(2)中的三角函数作近似处理,只能适合于小角度的坐标转换,而船舶测量中各站间的坐标系为任意角度,故本文采取线性化方式将式(2),式(4),式(5)在近似值处用泰勒公式展开进行线性化。此处近似值根据罗德里格矩阵的算法,选择相邻两测站间的2个公共点(因为缩放系数设为1),计算出转换参数的初始值。
4 算例分析
由于船舶测量中关心的数据是构件本身尺寸而非构件的绝对坐标,所以本例中设站均为自由设站,坐标系为测站本身的坐标系。所测数据为实验室中某一构件标定点坐标,该构件高约3m,宽约8m,紧贴墙壁竖立于实验室中,构件上有已经标定过的60个不同分散的坐标点。公共点的选取为任意可观测到的坐标点,选取的坐标点尽量分散开。
本例中使用的全站仪型号为索佳 NET05,3D 精密自动化全站仪,其标称测角精度为
0.5″,测距精度为0.5mm+1ppm。本例共设4个测站,即有4套不同的坐标系
,相邻测站间有5个公共点。目前日韩船舶搭载中,大合拢间隙基本控制在5±3mm,最大为12mm。以 Matlab为计算平台,由于限制条件中出现累加、累乘的现象,需要使用 Matlab进行循环计算。根据采集到的数据,先将相邻两测站间的公共点运用罗德里格矩阵法,计算出转换参数的初值。然后运用编写好的 Matlab程序读入初值和所有公共点坐标,实际计算过程中,任意两个相邻测站的转换参数的初值和该两测站间的公共点是对应的。通过不断的迭代进行整体平差,迭代过程中设置阀值,当转换参数的精度达到预期要求时退出迭代,计算完成,输出转换参数的结果。
5 结论
自由移站方法,可以选择任意合适的位置进行设站,且不需要对中,可方便有效地应用于船舶构件的测量工作。对于大范围的精密工程测量也可以推广使用,将其中任意一个测站坐标系与已知坐标系进行精密衔接,通过转换参数便可将各站自由设站中所测的坐标点统一归算到已知坐标系。文中通过对多站转换参数进行整体平差,提高了转换参数的精度,弥补了由于自由设站数量增加而造成的转换参数精度损失,坐标转换精度满足造船业的需求。
张 鹏 等《一 种 基 于 严 密 平 差 的 大 尺 寸 移 站 测 量 算 法》2013年
摘 要:针对船舶建造行业大尺寸工业构件高精度的控制需求,研究了利用基于严密平差的移站测量算法提高精度的方法,并在移站测量实现不可见点采集的基础上,将不同测站采集的数据进行严密平差处理,以降低移站累计误差,保证大尺寸构件的建造精度,从而提高船体建造质量。
0 引言
随着船舶建造业的发展,精度控制成为影响造船质量的关键因素。特别是在大尺寸构件的生产装配中,高精度的控制方法已成为造船人员不断研究改进的重点。对于船舶等大尺寸构件,
由于其体积大,通常无法在一个测站完成全部测量工作,移站测量法是近年应用广泛的一种直接统一多站坐标的方法[1],该方法精度高,可直接将不同测站所测坐标归算至选定坐标系下,避免了建立控制网和大量的后处理工作,还可根据采集数据及时判定点位偏差,进行现场校核,较好的解决了大尺寸测量问题[2]。但由于每次移站都会有移站误差,多次移站后的测站累计误差将不可忽略,本文在研究移站测量的基础上,提出一种通过测站回归闭合的方法,对全部测站数据进行整体平差,以降低转站误差,提高测点精度。
1. 1 移站测量观测误差模型
不同测站进行坐标测量时,测量仪器均是通过测站坐标以及对目标点的基本观测量(斜距、水平角、天顶距)来计算目标点的坐标值。本文现推导以全站仪观测量斜距、水平角
、天顶距获取测站点坐标的三维平差方法。
1) 斜距误差方程。
2) 水平方位角误差方程。
3) 天顶距误差方程。
张卡等《三维坐标转换的两种方法及其比较研究》2008年
摘要:针对7参数法三维坐标转换问题,对比分析了传统的基于泰勒级数展开的线性模型转换方法和基于罗德里格矩阵的三维坐标转换方法.由于在基于罗德里格矩阵的转换方法中,不需进行三角函数的计算,也不需迭代计算,因而其计算速度更快;而且其解决了线性模型对旋转角大小的限制,不仅适用于小角度的空间直角坐标转换,也能用于大角度的空间坐标转换.实脸结果也表明基于罗德里格矩阵的转换方法具有更好的适用性和更高的精度.
为了计算方便,对所用到的公共点坐标进行重心化处理,将两个坐标系的公共点的坐标均化算为以重心为原点的重心化坐标
将公共点的重心化坐标代人式(1),可得:
因而,转换参数可分两步来求解,即先用式(3)求出旋转参数和比例因子,再用式(4)求出平移参数.
1.1基于泰勒级数展开的转换方法
1.2基于罗德里格矩阵的转换方法
3结论
从实验结果可看出,对于小角度的空间坐标转换(第一组实验数据),基于泰勒级数展开的方法和基于罗德里格矩阵的方法的解算结果相当,都可以得到较好的转换结果;而对于大角度的空间坐标转换(第二组实验数据),由于基于泰勒级数展开的方法中,旋转参数的初始值偏离真值较大,因而其完全得不到正确的结果,但基于罗德里格矩阵的转换方法,不涉及泰勒级数展开和旋转参数初始值的选取,实现了纯线性化方法解决非线性约束问题的思想,因而其依然能得到很高的转换精度.另外,在基于罗德里格矩阵的方法中,不需要计算复杂的三角函数,也不需迭代运算,计算过程简单明了.因此,当两个坐标系间的旋转角较大时, 传统的基于泰勒级数展开的线性模型转换方法存在很大的模型误差,无法适用;而基于罗德里格矩阵的坐标转换方法,对坐标系间的旋转角大小没有限制,算法简单而有效,具有更好的适用性.
潘国荣等《两种大转角空间坐标转换模型研究》
摘 要:空间大转角的坐标转换,可以采用由适用于小角度转换的布尔莎模型改进的七参数模型,也可以采用罗德里格矩阵转换法来实现。本研究针对两种方法的原理和适用条件,通过模拟实验和在地铁盾构工程实例中对两种坐标转换模型的解算过程和结果进行分析和比较,得出以下结论:在大旋转角情况下,罗德里格矩阵转换模型作为非迭代模型算法简明,不受旋转角度的限制,易于快速实现,适用于常规精度要求的工程应用;改进的七参数迭代模型,算法严密,精度更高,实现大旋转角坐标转换的过程复杂,适用于高精度要求的研究应用。
常用的七参数模型,其旋转矩阵R 通常由两套坐标系的坐标轴夹角α,β,γ 表示,优点是精度较高,但算法较复杂,需要线性化。基于罗德里格矩阵的坐标转换模型的旋转矩阵 R 由罗德里格矩阵的3个独立参数组成,文献[4]指出该模型优点是算法简明,稳定性强,但转换参数需要逐步解算,算法严密性不高,在某些情况下所表示的三维旋转矩阵是奇异的。
文献[5]提出,当旋转角度大于0.5°时布尔莎模型的均方误差便明显大于罗格里德矩阵坐标转换法,因此需要将布尔莎模型进行泰勒展开导出适用于大角度的七参数模型。文献[6]尝试在更大旋转角情况下比较两种模型的精度,但其从布尔莎模型导出的七参数模型精度太低,认为在大角度情况下与罗德里格矩阵转换法没有可比较性。文献[7]提出适用于大旋转角的高精度的七参数迭代模型,为七参数模型在大旋转角下的精度研究提供了理论基础。本研究针对大旋转角的七参数模型和基于罗德里矩阵的坐标转换模型,比较它们的区别和特点,通过编程实现转换并对两种模型进行精度评定。
1.1 七参数模型
1.2 基于罗德里格矩阵的坐标转换模型
2 算例和精度评定
由表1可知,在观测误差为1mm 的大旋转角情况下,两种坐标转换方法求得的参数值与真值偏差不大,且七参数模型的参数解更接近真值。
由表2可知,在观测数据含有随机误差,大旋转角情况下,七参数迭代模型精度略高于基于罗德里格矩阵的坐标转换模型精度,可见基于罗德里格矩阵的坐标转换模型在求解参数时存在误差传递,对坐标转换精度有一定影响。
表5中,七参数模型和基于罗德里格矩阵的转换模型计算出的尺度参数和位移参数相差很大。当七参数模型选取不同的参数迭代初值时,将导致解算出的参数值变化很大[6],原因是受到在旋转矩阵 R 线性化过程中未考虑旋转角象限等因素的影响。而这种参数值的变化是相互适应的,利用它们所求得的坐标转换结果一致。
4 结论
对于大角度的空间坐标转换,七参数迭代模型和基于罗德里格矩阵的坐标转换模型都可以得到令人满意的结果。两种参数模型采用不同的数学思想解决坐标转换问题,其中七参数迭代模型采用平差方法,能使含有随机误差的观测数据的残差满足最小二乘原则,其精度略高于采用纯数学方法的罗德里格矩阵转换模型,但七参数模型作为一种局部最优解方法,线性化过程较为复杂,需要考虑旋转角的象限问题,工作量较大。而罗德里格矩阵转换方法由于不需要计算复杂的三角函数和迭代运算,与七参数模型相比工作量较少,更容易实现,虽然由于误差传递其精度略低于七参数迭代模型,但足以满足常规工程需要。
秦世伟等《任意旋转角坐标转换的简便模型》2009年
摘要:本文提出了一种适合于任意旋转角坐标转换的简便模型,该模型的原理是首先对两套坐标系下各点的坐标进行重心化,而后求得转换矩阵。在一个模拟算例和一个工程实例中应用本文的方法进行坐标转换并对结果进行分析和比较,说明了本文提出的简便方法的实施过程和有效性。将本文提出的方法用于地铁盾构的姿态控制,取得了令人满意的效果。
重心化
不妨设在O-XYZ坐标系中的n个点的三维坐标表示为A,在o-xyz坐标系中表示为B,其中,
4 结语
本文提出了一种适合任意旋转角的坐标转换的简便模型。同现有的坐标转换方法相比,本文提出的方法具有简便快捷、精度较高的特点,其最大的运算仅是一个3阶矩阵的求逆,手工计算即可完成,采用一个模拟算例研究了本文模型的精度和可靠性,认为在大于等于4个点的情况下,本文的坐标转换模型能够取得满意的效果。用一个已发表文献中的工程实例,将本文方法得到的坐标转换结果同原文的坐标转换结果进行比较,得出本文的转换模型能够取得与参考文献中的大旋转角13参数模型等价的结果,但是本文提出的模型的运算量和复杂程度大大降低。
将本文提出的方法应用到地铁盾构姿态控制中,实际应用结果表明,本文提出的坐标转换模型具有较好的实用价值。
陈义等《适用于大旋转角的三维基准转换的一种简便模型》 2004年
此文是上文的文献6
其实就是13参数转换方法
适用范围:
在上述模型中,给出的约束条件是正交条件,因此,只要满足正交条件,任意坐标系都可以进行相互转换,也就是它适用于左手系、右手系、左右手系之间的相互转换。对于左右手系之间的转换,除了应满足左手系、右手系相互转换的正交矩阵外,还要乘上一个坐标轴反向矩阵。坐标轴反向矩阵也是一个正交矩阵,正交矩阵相乘还是正交矩阵,因此,本模型同样适用于左右手系之间的转换。限于篇幅,本文未写粗差剔除的原理和计算方法,但在软件中已经实现了粗差剔除的功能,并取得了很好的效果。
3结 语
1)本方法将空间直角坐标转换问题从非线性的、参数独立的形式转化为准线性的、参数相关的形式,使解算公式简单明了。
2)本方法适用于任意角度的旋转,而无需预先知道旋转角度的近似值。一般可假设旋转矩阵
的初始状态为单位阵。
3)本方法同样适用于左、右手系坐标之间的转换。
4)经过模拟数据和实测数据的验证,本方法具有解算精度高、收敛速度快、程序编制方便、
使用灵活等特点。它适用于大地测量、摄影测量、工程测量等领域。

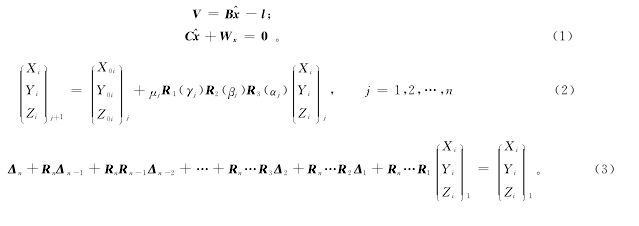
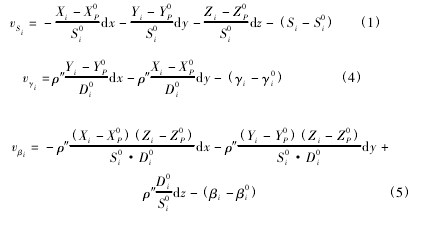
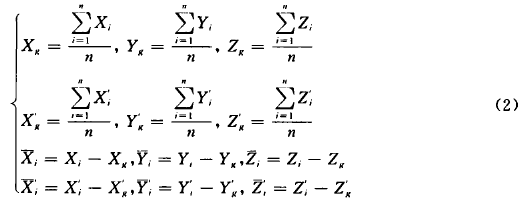
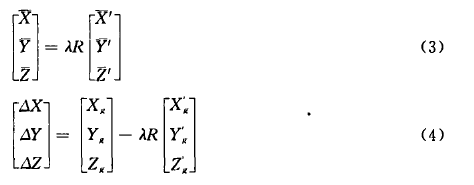
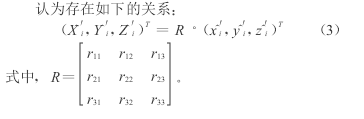


发表评论: